Portal:Mathematics

The Mathematics Portal

Isaac Newton

Mathematics is the study of representing and reasoning about abstract objects (such as numbers, points, spaces, sets, structures, and games). Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered. (Full article...)

Featured articles –

  Featured articles are displayed here, which represent some of the best content on English Wikipedia.

---

• 
  
  

  

  Hilary Putnam

  
  The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.
  
  Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...)
• 

  

  
  Richard Phillips Feynman (/ˈfaɪnmən/; May 11, 1918 – February 15, 1988) was an American theoretical physicist. He is known for the work he did in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, and in particle physics, for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.
  
  Feynman developed a widely used pictorial representation scheme for the mathematical expressions describing the behavior of subatomic particles, which later became known as Feynman diagrams. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World, he was ranked the seventh-greatest physicist of all time. (Full article...)
• 
  
  

  

  Elementary algebra studies which values solve equations formed using arithmetical operations.

  
  Algebra is the branch of mathematics that studies certain abstract systems, known as algebraic structures, and the manipulation of statements within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations such as addition and multiplication.
  
  Elementary algebra is the main form of algebra taught in school and examines mathematical statements using variables for unspecified values. It seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. (Full article...)
• 
  
  

  

  The title page of a 1634 version of Hues' Tractatus de globis in the collection of the Biblioteca Nacional de Portugal

  
  Robert Hues (1553 – 24 May 1632) was an English mathematician and geographer. He attended St. Mary Hall at Oxford, and graduated in 1578. Hues became interested in geography and mathematics, and studied navigation at a school set up by Walter Raleigh. During a trip to Newfoundland, he made observations which caused him to doubt the accepted published values for variations of the compass. Between 1586 and 1588, Hues travelled with Thomas Cavendish on a circumnavigation of the globe, performing astronomical observations and taking the latitudes of places they visited. Beginning in August 1591, Hues and Cavendish again set out on another circumnavigation of the globe. During the voyage, Hues made astronomical observations in the South Atlantic, and continued his observations of the variation of the compass at various latitudes and at the Equator. Cavendish died on the journey in 1592, and Hues returned to England the following year.
  
  In 1594, Hues published his discoveries in the Latin work Tractatus de globis et eorum usu (Treatise on Globes and Their Use) which was written to explain the use of the terrestrial and celestial globes that had been made and published by Emery Molyneux in late 1592 or early 1593, and to encourage English sailors to use practical astronomical navigation. Hues' work subsequently went into at least 12 other printings in Dutch, English, French and Latin. (Full article...)
• 
  
  

  

  One of Molyneux's celestial globes, which is displayed in Middle Temple Library – from the frontispiece of the Hakluyt Society's 1889 reprint of A Learned Treatise of Globes, both Cœlestiall and Terrestriall, one of the English editions of Robert Hues' Latin work Tractatus de Globis (1594)

  
  Emery Molyneux (/ˈɛməri ˈmɒlɪnoʊ/ EM-ər-ee MOL-in-oh; died June 1598) was an English Elizabethan maker of globes, mathematical instruments and ordnance. His terrestrial and celestial globes, first published in 1592, were the first to be made in England and the first to be made by an Englishman.
  
  Molyneux was known as a mathematician and maker of mathematical instruments such as compasses and hourglasses. He became acquainted with many prominent men of the day, including the writer Richard Hakluyt and the mathematicians Robert Hues and Edward Wright. He also knew the explorers Thomas Cavendish, Francis Drake, Walter Raleigh and John Davis. Davis probably introduced Molyneux to his own patron, the London merchant William Sanderson, who largely financed the construction of the globes. When completed, the globes were presented to Elizabeth I. Larger globes were acquired by royalty, noblemen and academic institutions, while smaller ones were purchased as practical navigation aids for sailors and students. The globes were the first to be made in such a way that they were unaffected by the humidity at sea, and they came into general use on ships. (Full article...)
• 
  
  

  

  Noether c. 1900–1910

  
  Amalie Emmy Noether (US: /ˈnʌtər/, UK: /ˈnɜːtə/; German: [ˈnøːtɐ]; 23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She proved Noether's first and second theorems, which are fundamental in mathematical physics. She was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.
  
  Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations but instead studied mathematics at the University of Erlangen, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, however, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. (Full article...)
• 

  

  
  Émile Michel Hyacinthe Lemoine (French: [emil ləmwan]; 22 November 1840 – 21 February 1912) was a French civil engineer and a mathematician, a geometer in particular. He was educated at a variety of institutions, including the Prytanée National Militaire and, most notably, the École Polytechnique. Lemoine taught as a private tutor for a short period after his graduation from the latter school.
  
  Lemoine is best known for his proof of the existence of the Lemoine point (or the symmedian point) of a triangle. Other mathematical work includes a system he called Géométrographie and a method which related algebraic expressions to geometric objects. He has been called a co-founder of modern triangle geometry, as many of its characteristics are present in his work. (Full article...)
• 
  
  

  

  Kaczynski after his arrest in 1996

  
  Theodore John Kaczynski (/kəˈzɪnski/ kə-ZIN-skee; May 22, 1942 – June 10, 2023), also known as the Unabomber (/ˈjuːnəbɒmər/ YOO-nə-bom-ər), was an American mathematician and domestic terrorist. He was a mathematics prodigy, but abandoned his academic career in 1969 to pursue a reclusive primitive lifestyle.
  
  Kaczynski murdered three people and injured 23 others between 1978 and 1995 in a nationwide mail bombing campaign against people he believed to be advancing modern technology and the destruction of the natural environment. He authored Industrial Society and Its Future, a 35,000-word manifesto and social critique which opposes all forms of technology, rejecting leftism, and advocating a nature-centered form of anarchism. (Full article...)
• 

  

  The regular triangular tiling of the plane, whose symmetries are described by the affine symmetric group S̃₃

  
  The affine symmetric groups are a family of mathematical structures that describe the symmetries of the number line and the regular triangular tiling of the plane, as well as related higher-dimensional objects. In addition to this geometric description, the affine symmetric groups may be defined in other ways: as collections of permutations (rearrangements) of the integers (..., −2, −1, 0, 1, 2, ...) that are periodic in a certain sense, or in purely algebraic terms as a group with certain generators and relations. They are studied in combinatorics and representation theory.
  
  A finite symmetric group consists of all permutations of a finite set. Each affine symmetric group is an infinite extension of a finite symmetric group. Many important combinatorial properties of the finite symmetric groups can be extended to the corresponding affine symmetric groups. Permutation statistics such as descents and inversions can be defined in the affine case. As in the finite case, the natural combinatorial definitions for these statistics also have a geometric interpretation. (Full article...)
• 
  
  

  

  Rejewski, c. 1932

  
  Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.
  
  Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...)
• 
  
  

  

  A stamp of Zhang Heng issued by China Post in 1955

  
  Zhang Heng (Chinese: 張衡; AD 78–139), formerly romanized Chang Heng, was a Chinese polymathic scientist and statesman who lived during the Han dynasty. Educated in the capital cities of Luoyang and Chang'an, he achieved success as an astronomer, mathematician, seismologist, hydraulic engineer, inventor, geographer, cartographer, ethnographer, artist, poet, philosopher, politician, and literary scholar.
  
  Zhang Heng began his career as a minor civil servant in Nanyang. Eventually, he became Chief Astronomer, Prefect of the Majors for Official Carriages, and then Palace Attendant at the imperial court. His uncompromising stance on historical and calendrical issues led to his becoming a controversial figure, preventing him from rising to the status of Grand Historian. His political rivalry with the palace eunuchs during the reign of Emperor Shun (r. 125–144) led to his decision to retire from the central court to serve as an administrator of Hejian Kingdom in present-day Hebei. Zhang returned home to Nanyang for a short time, before being recalled to serve in the capital once more in 138. He died there a year later, in 139. (Full article...)
• 
  
  

  

  Portrait by August Köhler, c. 1910, after 1627 original

  
  Johannes Kepler (/ˈkɛplər/; German: [joˈhanəs ˈkɛplɐ, -nɛs -] ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium.
  
  Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein.
  Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. (Full article...)
• 

  

  
  Josiah Willard Gibbs (/ɡɪbz/; February 11, 1839 – April 28, 1903) was an American scientist who made significant theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in transforming physical chemistry into a rigorous deductive science. Together with James Clerk Maxwell and Ludwig Boltzmann, he created statistical mechanics (a term that he coined), explaining the laws of thermodynamics as consequences of the statistical properties of ensembles of the possible states of a physical system composed of many particles. Gibbs also worked on the application of Maxwell's equations to problems in physical optics. As a mathematician, he created modern vector calculus (independently of the British scientist Oliver Heaviside, who carried out similar work during the same period) and described the Gibbs phenomenon in the theory of Fourier analysis.
  
  In 1863, Yale University awarded Gibbs the first American doctorate in engineering. After a three-year sojourn in Europe, Gibbs spent the rest of his career at Yale, where he was a professor of mathematical physics from 1871 until his death in 1903. Working in relative isolation, he became the earliest theoretical scientist in the United States to earn an international reputation and was praised by Albert Einstein as "the greatest mind in American history". In 1901, Gibbs received what was then considered the highest honor awarded by the international scientific community, the Copley Medal of the Royal Society of London, "for his contributions to mathematical physics". (Full article...)
• 

  

  Figure 1: A solution (in purple) to Apollonius's problem. The given circles are shown in black.

  
  
  In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga (c. 262 BC – c. 190 BC) posed and solved this famous problem in his work Ἐπαφαί (Epaphaí, "Tangencies"); this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets (there are 4 ways to divide a set of cardinality 3 in 2 parts).
  
  In the 16th century, Adriaan van Roomen solved the problem using intersecting hyperbolas, but this solution does not use only straightedge and compass constructions. François Viète found such a solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius (a point) or expanded to infinite radius (a line). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN. (Full article...)
• 
  
  

  

  Cantor, c. 1910

  
  Georg Ferdinand Ludwig Philipp Cantor (/ˈkæntɔːr/ KAN-tor; German: [ˈɡeːɔʁk ˈfɛʁdinant ˈluːtvɪç ˈfiːlɪp ˈkantoːɐ̯]; 3 March [O.S. 19 February] 1845 – 6 January 1918) was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.
  
  Originally, Cantor's theory of transfinite numbers was regarded as counter-intuitive – even shocking. This caused it to encounter resistance from mathematical contemporaries such as Leopold Kronecker and Henri Poincaré and later from Hermann Weyl and L. E. J. Brouwer, while Ludwig Wittgenstein raised philosophical objections; see Controversy over Cantor's theory. Cantor, a devout Lutheran Christian, believed the theory had been communicated to him by God. Some Christian theologians (particularly neo-Scholastics) saw Cantor's work as a challenge to the uniqueness of the absolute infinity in the nature of God – on one occasion equating the theory of transfinite numbers with pantheism – a proposition that Cantor vigorously rejected. Not all theologians were against Cantor's theory; prominent neo-scholastic philosopher Constantin Gutberlet was in favor of it and Cardinal Johann Baptist Franzelin accepted it as a valid theory (after Cantor made some important clarifications). (Full article...)

Selected image –

animation of the construction of a fourth-degree Bézier curve

Bézier curve

Credit: Phil Tregoning

A Bézier curve is a parametric curve important in computer graphics and related fields. Widely publicized in 1962 by the French engineer Pierre Bézier, who used them to design automobile bodies, the curves were first developed in 1959 by Paul de Casteljau using de Casteljau's algorithm. In this animation, a quartic Bézier curve is constructed using control points P₀ through P₄. The green line segments join points moving at a constant rate from one control point to the next; the parameter t shows the progress over time. Meanwhile, the blue line segments join points moving in a similar manner along the green segments, and the magenta line segment points along the blue segments. Finally, the black point moves at a constant rate along the magenta line segment, tracing out the final curve in red. The curve is a fourth-degree function of its parameter. Quadratic and cubic Bézier curves are most common since higher-degree curves are more computationally costly to evaluate. When more complex shapes are needed, lower-order Bézier curves are patched together. For example, modern computer fonts use Bézier splines composed of quadratic or cubic Bézier curves to create scalable typefaces. The curves are also used in computer animation and video games to plot smooth paths of motion. Approximate Bézier curves can be generated in the "real world" using string art.

Good articles –

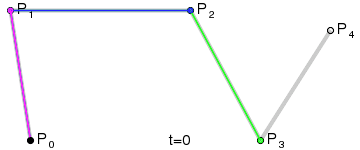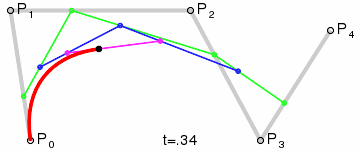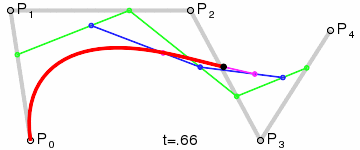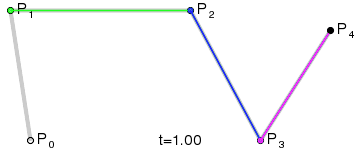
  These are Good articles, which meet a core set of high editorial standards.

---

• 

  

  Composite numbers can be arranged into rectangles but prime numbers cannot.

  
  
  A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order.
  
  The property of being prime is called primality. A simple but slow method of checking the primality of a given number $n$, called trial division, tests whether $n$ is a multiple of any integer between 2 and ${\sqrt {n}}$. Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which always produces the correct answer in polynomial time but is too slow to be practical. Particularly fast methods are available for numbers of special forms, such as Mersenne numbers. As of October 2024 the largest known prime number is a Mersenne prime with 41,024,320 decimal digits. (Full article...)
• 

  

  The integer number line, a set of infinitely many points with integer distances. According to the Erdős–Anning theorem, any such set lies on a line.

  
  The Erdős–Anning theorem states that, whenever an infinite number of points in the plane all have integer distances, the points lie on a straight line. The same result holds in higher dimensional Euclidean spaces.
  The theorem cannot be strengthened to give a finite bound on the number of points: there exist arbitrarily large finite sets of points that are not on a line and have integer distances.
  
  The theorem is named after Paul Erdős and Norman H. Anning, who published a proof of it in 1945. Erdős later supplied a simpler proof, which can also be used to check whether a point set forms an Erdős–Diophantine graph, an inextensible system of integer points with integer distances. The Erdős–Anning theorem inspired the Erdős–Ulam problem on the existence of dense point sets with rational distances. (Full article...)
• 

  

  Fibonacci nim is played with a pile of coins. The number of coins in this pile, 21, is a Fibonacci number, so a game starting with this pile and played optimally will be won by the second player.

  
  Fibonacci nim is a mathematical subtraction game, a variant of the game of nim. Players alternate removing coins from a pile, on each move taking at most twice as many coins as the previous move, and winning by taking the last coin. The Fibonacci numbers feature heavily in its analysis; in particular, the first player can win if and only if the starting number of coins is not a Fibonacci number. A complete strategy is known for best play in games with a single pile of counters, but not for variants of the game with multiple piles. (Full article...)
• 

  

  Kissing circles. Given three mutually tangent circles (black), there are, in general, two possible answers (red) as to what radius a fourth tangent circle can have.

  
  In geometry, Descartes' theorem states that for every four kissing, or mutually tangent, circles, the radii of the circles satisfy a certain quadratic equation. By solving this equation, one can construct a fourth circle tangent to three given, mutually tangent circles. The theorem is named after René Descartes, who stated it in 1643.
  
  Frederick Soddy's 1936 poem The Kiss Precise summarizes the theorem in terms of the bends (signed inverse radii) of the four circles: (Full article...)
• 
  
  

  

  L6a4

  
  In mathematics, the Borromean rings are three simple closed curves in three-dimensional space that are topologically linked and cannot be separated from each other, but that break apart into two unknotted and unlinked loops when any one of the three is cut or removed. Most commonly, these rings are drawn as three circles in the plane, in the pattern of a Venn diagram, alternatingly crossing over and under each other at the points where they cross. Other triples of curves are said to form the Borromean rings as long as they are topologically equivalent to the curves depicted in this drawing.
  
  The Borromean rings are named after the Italian House of Borromeo, who used the circular form of these rings as an element of their coat of arms, but designs based on the Borromean rings have been used in many cultures, including by the Norsemen and in Japan. They have been used in Christian symbolism as a sign of the Trinity, and in modern commerce as the logo of Ballantine beer, giving them the alternative name Ballantine rings. Physical instances of the Borromean rings have been made from linked DNA or other molecules, and they have analogues in the Efimov state and Borromean nuclei, both of which have three components bound to each other although no two of them are bound. (Full article...)
• 

  

  Six points in the unit square, with the smallest triangles (red) having area 1/8, the optimal area for this number of points. Other larger triangles are colored blue. These points are an affine transformation of a regular hexagon, but for larger numbers of points the optimal solution does not form a convex polygon.

  
  In discrete geometry and discrepancy theory, the Heilbronn triangle problem is a problem of placing points in the plane, avoiding triangles of small area. It is named after Hans Heilbronn, who conjectured that, no matter how points are placed in a given area, the smallest triangle area will be at most inversely proportional to the square of the number of points. His conjecture was proven false, but the asymptotic growth rate of the minimum triangle area remains unknown. (Full article...)
• 

  

  Rule 184, run for 128 steps from random configurations with each of three different starting densities: top 25%, middle 50%, bottom 75%. The view shown is a 300-pixel crop from a wider simulation.

  
  Rule 184 is a one-dimensional binary cellular automaton rule, notable for solving the majority problem as well as for its ability to simultaneously describe several, seemingly quite different, particle systems:
  

  • Rule 184 can be used as a simple model for traffic flow in a single lane of a highway, and forms the basis for many cellular automaton models of traffic flow with greater sophistication. In this model, particles (representing vehicles) move in a single direction, stopping and starting depending on the cars in front of them. The number of particles remains unchanged throughout the simulation. Because of this application, Rule 184 is sometimes called the "traffic rule".
  • Rule 184 also models a form of deposition of particles onto an irregular surface, in which each local minimum of the surface is filled with a particle in each step. At each step of the simulation, the number of particles increases. Once placed, a particle never moves.
  • Rule 184 can be understood in terms of ballistic annihilation, a system of particles moving both leftwards and rightwards through a one-dimensional medium. When two such particles collide, they annihilate each other, so that at each step the number of particles remains unchanged or decreases.

  
  The apparent contradiction between these descriptions is resolved by different ways of associating features of the automaton's state with particles. (Full article...)
• 

  

  
  In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Perhaps most familiar as a property of arithmetic, e.g. "3 + 4 = 4 + 3" or "2 × 5 = 5 × 2", the property can also be used in more advanced settings. The name is needed because there are operations, such as division and subtraction, that do not have it (for example, "3 − 5 ≠ 5 − 3"); such operations are not commutative, and so are referred to as noncommutative operations. The idea that simple operations, such as the multiplication and addition of numbers, are commutative was for many years implicitly assumed. Thus, this property was not named until the 19th century, when mathematics started to become formalized. A similar property exists for binary relations; a binary relation is said to be symmetric if the relation applies regardless of the order of its operands; for example, equality is symmetric as two equal mathematical objects are equal regardless of their order. (Full article...)
• 
  The Earth–Moon problem is an unsolved problem on graph coloring in mathematics. It is an extension of the planar map coloring problem (solved by the four color theorem), and was posed by Gerhard Ringel in 1959. An intuitive form of the problem asks how many colors are needed to color political maps of the Earth and Moon, in a hypothetical future where each Earth country has a Moon colony which must be given the same color. In mathematical terms, it seeks the chromatic number of biplanar graphs. It is known that this number is at least 9 and at most 12.
  
  The Earth–Moon problem has been extended to analogous problems of coloring maps on any number of planets. For this extension the lower bounds and upper bounds on the number of colors are closer, within two of each other. One real-world application of the Earth–Moon problem involves testing printed circuit boards. (Full article...)
• 
  
  

  

  An example of non‑periodicity due to another orientation of one tile out of an infinite number of identical tiles

  
  A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.
  
  A periodic tiling has a repeating pattern. Some special kinds include regular tilings with regular polygonal tiles all of the same shape, and semiregular tilings with regular tiles of more than one shape and with every corner identically arranged. The patterns formed by periodic tilings can be categorized into 17 wallpaper groups. A tiling that lacks a repeating pattern is called "non-periodic". An aperiodic tiling uses a small set of tile shapes that cannot form a repeating pattern (an aperiodic set of prototiles). A tessellation of space, also known as a space filling or honeycomb, can be defined in the geometry of higher dimensions. (Full article...)
• 

  

  Translation of an English sentence to first-order logic

  
  
  Logic translation is the process of representing a text in the formal language of a logical system. If the original text is formulated in ordinary language then the term natural language formalization is often used. An example is the translation of the English sentence "some men are bald" into first-order logic as $\exists x(M(x)\land B(x))$. The purpose is to reveal the logical structure of arguments. This makes it possible to use the precise rules of formal logic to assess whether these arguments are correct. It can also guide reasoning by arriving at new conclusions.
  
  Many of the difficulties of the process are caused by vague or ambiguous expressions in natural language. For example, the English word "is" can mean that something exists, that it is identical to something else, or that it has a certain property. This contrasts with the precise nature of formal logic, which avoids such ambiguities. Natural language formalization is relevant to various fields in the sciences and humanities. It may play a key role for logic in general since it is needed to establish a link between many forms of reasoning and abstract logical systems. The use of informal logic is an alternative to formalization since it analyzes the cogency of ordinary language arguments in their original form. Natural language formalization is distinguished from logic translations that convert formulas from one logical system into another, for example, from modal logic to first-order logic. This form of logic translation is specifically relevant for logic programming and metalogic. (Full article...)
• 
  In the mathematical fields of graph theory and finite model theory, the logic of graphs deals with formal specifications of graph properties using sentences of mathematical logic. There are several variations in the types of logical operation that can be used in these sentences. The first-order logic of graphs concerns sentences in which the variables and predicates concern individual vertices and edges of a graph, while monadic second-order graph logic allows quantification over sets of vertices or edges. Logics based on least fixed point operators allow more general predicates over tuples of vertices, but these predicates can only be constructed through fixed-point operators, restricting their power.
  
  A sentence $S$ may be true for some graphs, and false for others; a graph $G$ is said to model $S$, written $G\models S$, if $S$ is true of the vertices and adjacency relation of $G$. The algorithmic problem of model checking concerns testing whether a given graph models a given sentence. The algorithmic problem of satisfiability concerns testing whether there exists a graph that models a given sentence.
  Although both model checking and satisfiability are hard in general, several major algorithmic meta-theorems show that properties expressed in this way can be tested efficiently for important classes of graphs. (Full article...)

Did you know (auto-generated) –

• ... that Fairleigh Dickinson's upset victory over Purdue was the biggest upset in terms of point spread in NCAA tournament history, with Purdue being a 23+1⁄2-point favorite?
• ... that The Math Myth advocates for American high schools to stop requiring advanced algebra?
• ... that Ukrainian baritone Danylo Matviienko, who holds a master's degree in mathematics, appeared as Demetrius in Britten's opera A Midsummer Night's Dream at the Oper Frankfurt?
• ... that after Florida schools banned 54 mathematics books, Chaz Stevens petitioned that they also ban the Bible?
• ... that the music of math rock band Jyocho has been alternatively described as akin to "madness" or "contemplative and melancholy"?
• ... that the prologue to The Polymath was written by Martin Kemp, a leading expert on Leonardo da Vinci?
• ... that the British National Hospital Service Reserve trained volunteers to carry out first aid in the aftermath of a nuclear or chemical attack?
• ... that people in Madagascar perform algebra on tree seeds in order to tell the future?

More did you know –

Did you know...

• ...that i to the power of i, where i is the square root of -1, is a real number?
• ...an infinite, nonrepeating decimal can be represented using only the number 1 using continued fractions?
• ...that 253931039382791 and the following 18 prime numbers all end in the digit 1?
• ...that the Electronic Frontier Foundation funds awards for the discovery of prime numbers beyond certain sizes?
• ...that pi can be computed using only the number 2 by the work of Viète?
• … that the Riemann Hypothesis, one of the Millennium Problems, depends on the asymptotic growth of the Mertens Function?
• … that every positive integer can be written as the sum of three palindromic numbers in every number system with base 5 or greater?

Selected article –

The real part (red) and imaginary part (blue) of the critical line Re(s) = 1/2 of the Riemann zeta-function. Image credit: User:Army1987

The Riemann hypothesis, first formulated by Bernhard Riemann in 1859, is one of the most famous unsolved problems. It has been an open question for well over a century, despite attracting concentrated efforts from many outstanding mathematicians.

The Riemann hypothesis is a conjecture about the distribution of the zeros of the Riemann zeta-function ζ(s). The Riemann zeta-function is defined for all complex numbers s ≠ 1. It has zeros at the negative even integers (i.e. at s=-2, s=-4, s=-6, ...). These are called the trivial zeros. The Riemann hypothesis is concerned with the non-trivial zeros, and states that:

The real part of any non-trivial zero of the Riemann zeta function is ½

Thus the non-trivial zeros should lie on the so-called critical line ½ + it with t a real number and i the imaginary unit. The Riemann zeta-function along the critical line is sometimes studied in terms of the Z-function, whose real zeros correspond to the zeros of the zeta-function on the critical line.

The Riemann hypothesis is one of the most important open problems in contemporary mathematics; a $1,000,000 prize has been offered by the Clay Mathematics Institute for a proof. Most mathematicians believe the Riemann hypothesis to be true. (J. E. Littlewood and Atle Selberg have been reported as skeptical. Selberg's skepticism, if any, waned, from his young days. In a 1989 paper, he suggested that an analogue should hold for a much wider class of functions, the Selberg class.) (Full article...)

View all selected articles

Subcategories

Algebra | Arithmetic | Analysis | Complex analysis | Applied mathematics | Calculus | Category theory | Chaos theory | Combinatorics | Dynamical systems | Fractals | Game theory | Geometry | Algebraic geometry | Graph theory | Group theory | Linear algebra | Mathematical logic | Model theory | Multi-dimensional geometry | Number theory | Numerical analysis | Optimization | Order theory | Probability and statistics | Set theory | Statistics | Topology | Algebraic topology | Trigonometry | Linear programming

---

Mathematics | History of mathematics | Mathematicians | Awards | Education | Literature | Notation | Organizations | Theorems | Proofs | Unsolved problems

Full category tree. Select [►] to view subcategories.

Mathematics

Mathematics by country

Fields of mathematics

Mathematics-related lists

Mathematicians

Works about mathematics

Mathematics and art

Mathematical classification systems

Mathematical concepts

Mathematical constants

Mathematics and culture

Eponyms in mathematics

Mathematical examples

FL-Class Polyhedra articles

History of mathematics

Mathematical notation

Mathematical science occupations

Outlines of mathematics and logic

Philosophy of mathematics

Mathematical projects

Mathematical proofs

Pseudomathematics

Set index articles on mathematics

Mathematical terminology

Mathematical theorems

Mathematical tools

Mathematics stubs

Topics in mathematics

General	Foundations	Number theory	Discrete mathematics
Mathematicians History of mathematics Philosophy of mathematics Mathematical notation Mathematical beauty Mathematics education Glossary of mathematical symbols	Foundations of mathematics Mathematical logic Proof theory Gödel's incompleteness theorems Model theory Recursion theory Set theory Naive set theory Axiomatic set theory Category theory Topos theory	Number theory Algebraic number theory Analytic number theory Arithmetic Fundamental theorem of arithmetic Numbers Natural numbers Prime numbers Rational numbers Algebraic numbers	Discrete mathematics Combinatorics Combinatorial geometry Coding theory Combinatorial design Enumerative combinatorics Combinatorial optimization Graph theory Order theory Lattice theory Digital Signal Processing Theoretical computer science Computability theory Complexity theory
Algebra	Analysis	Geometry and topology	Applied mathematics
Algebra Elementary algebra Abstract algebra Group theory Ring theory Field theory Commutative algebra Geometric algebra Linear algebra Matrix theory Multilinear algebra Universal algebra Fundamental theorem of algebra	Analysis Calculus Fundamental theorem of calculus Vector calculus Geometric calculus Measure theory Real analysis Complex analysis Differential equations Ordinary differential equations Partial differential equations Integral equations Approximation theory Special functions Potential theory Harmonic analysis Fourier analysis Functional analysis Operator theory	Geometry Euclidean geometry Trigonometry Analytic geometry Non-Euclidean geometry Affine geometry Projective geometry Convex geometry Discrete geometry Algebraic geometry Differential geometry K theory Gauge theory Riemannian geometry Lie groups Topology General topology Algebraic topology Geometric topology Differential topology	Applied mathematics Mathematical modeling Mathematical physics Dynamical systems Control theory Calculus of variations Optimization Mathematical economics Game theory Mathematical finance Statistics Probability theory Stochastic processes Numerical analysis Cryptography Information theory

Index of mathematics articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Related portals

WikiProjects

The Mathematics WikiProject is the center for mathematics-related editing on Wikipedia. Join the discussion on the project's talk page.

Project pages

• Participants
• Current activity
• Manual of style
• Conventions

Essays

• Advice on using Wikipedia for mathematics self-study
• Proofs

Subprojects

• PlanetMath Exchange (Talk)
• Graphics (Talk)
• Article assessment (Talk)

Related projects

Computer science | Cryptography | Game theory | Numbers | Physics | Science | Statistics

Things you can do

• Create a new article: List of requested articles
• Add a new image: Image requests
• Expand an article: Mathematics stubs
• Lend your expertise: Expert attention needed

In other Wikimedia projects

The following Wikimedia Foundation sister projects provide more on this subject:

• 

  Commons
  Free media repository

• 

  Wikibooks
  Free textbooks and manuals

• 

  Wikidata
  Free knowledge base

• 

  Wikinews
  Free-content news

• 

  Wikiquote
  Collection of quotations

• 

  Wikisource
  Free-content library

• 

  Wikiversity
  Free learning tools

• 

  Wiktionary
  Dictionary and thesaurus

More portals

Discover Wikipedia using portals

• 

  List of all portals

• 

  The arts portal

• 

  Biography portal

• 

  Current events portal

• 

  Geography portal

• 

  History portal

• 

  Mathematics portal

• 

  Science portal

• 

  Society portal

• 

  Technology portal

• 

  Random portal

• 

  WikiProject Portals